今天520耶,然鹅并没有什么故事,反倒是校园湖里的龟龟都是齐刷刷地出来晒背,湖里的黑天鹅也都成双成对。
今天回顾一下最小生成树Kruskal算法,先以题目代入吧。
问题描述
给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :abs(xi - xj) + abs(yi - yj)。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
示例
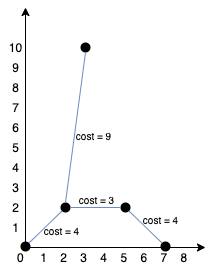
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出:20
分析
很典型的一个最小生成树问题。
由于给的都是点的坐标,首先定义一个Edge类,这个类有len,x,y属性,表示第x和第y个点的距离为len。遍历points可以得到一个Edge的集合,对该集合按照len属性的升序排序。初始化一个并查集,每个顶点自己为单独一个集合。Kruskal算法就是对升序的Edge集合进行遍历,每次遍历的时候看Edge涉及的两个顶点是不是连通的,如果不是连通的,则取该Edge为最小生成树组成部分,使用并查集将该两顶点合并;如果是连通的,则不对该Edge做处理。
代码如下
class Solution {
// 最小生成树 Kruskal
// 并查集
int[] pre;
public int minCostConnectPoints(int[][] points) {
int n = points.length;
pre = new int[n];
// 初始化并查集
for (int i = 0; i < n; i++) {
pre[i] = i;
}
// 遍历points,得到所有的边信息
List<Edge> edges = new ArrayList<>();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
edges.add(new Edge(dist(points, i, j), i, j));
}
}
// 对Edge按照len升序排序
Collections.sort(edges, (Edge e1, Edge e2) -> e1.len - e2.len);
int res = 0;
for (Edge e : edges) {
int len =e.len;
int x = e.x;
int y = e.y;
if (find(x) != find(y)) {
union(x, y);
res += len;
}
}
return res;
}
public int find(int root) {
if (pre[root] == root) {
return root;
}
return pre[root] = find(pre[root]);
}
public void union(int a, int b) {
int x = find(a);
int y = find(b);
if (x != y) {
pre[x] = y;
}
}
public int dist(int[][] points, int x, int y) {
return Math.abs(points[x][0] - points[y][0]) + Math.abs(points[x][1] - points[y][1]);
}
}
class Edge {
int len, x, y;
public Edge(int len, int x, int y) {
this.len = len;
this.x = x;
this.y = y;
}
}